بحث عن المتطابقات المثلثية يعتبر امر هام حيث أن المتطابقات المثلثية هي عبارة عن العلاقات الرياضية التي تربط بين زوايا المثلث وأضلاعه، وتستخدم في حل المثلثات وحساب المقادير المجهولة، يشمل ذلك النسب المثلثية الأساسية مثل الجيب، والظل، والقاطع، وغيرها، تستخدم هذه النسب للعثور على أطوال الأضلاع أو زوايا المثلث عندما يكون لدينا معلومات محددة عن بعض العناصر في المثلث.
جدول المحتويات
بحث عن المتطابقات المثلثية
علم حساب المثلثات يعتبر جزءاً هاماً من الرياضيات يهتم بدراسة العلاقات الهندسية بين زوايا المثلثات وأطوال الأضلاع فيها، يستخدم حساب المثلثات في العديد من المجالات العملية بشكل واسع، بما في ذلك قياس وتحديد الأبعاد في العديد من الأشكال الهندسية، وحساب المسافات والأرتفاعات في المهن المتعلقة بالهندسة المدنية والهندسة الكهربائية والهندسة الميكانيكية.
من الأمثلة العملية على استخدام حساب المثلثات:
- حساب ارتفاع الأشجار أو الأبراج باستخدام الزوايا والمسافات المعلومة.
- حساب ارتفاع الجبال أو التضاريس الأخرى باستخدام الزوايا والمسافات والأبعاد المعروفة.
- تحديد المسافات بين نقاط مختلفة على سطح الأرض باستخدام الزوايا والمثلثات.
- تطبيقات في الملاحة البحرية والطيران لتحديد المواقع والمسارات باستخدام حساب المثلثات.
من النسب المثلثية الأساسية:
- الجيب (جا)، وهو نسبة الضلع المقابل للزاوية المعينة إلى الوتر.
- الظل (ظا)، وهو نسبة الضلع المجاور للزاوية المعينة إلى الوتر.
- القاطع (قا)، وهو نسبة الضلع المقابل للزاوية المعينة إلى القاطع المجاور لها.
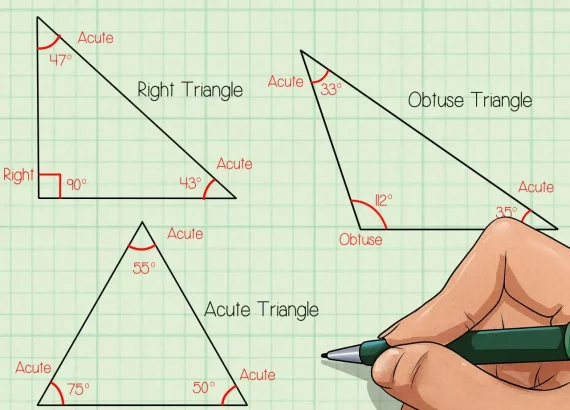
النسب المثلثية الأساسية
هذه النسب الثلاثة (الجيب، وجيب التمام، والظل) هي النسب الأساسية في المثلثات وتستخدم لحساب الزوايا والأطوال في المثلثات المختلفة، يمكن التعبير عن هذه النسب بالشكل التالي:
- الجيب (sin θ) يتم حسابه كنسبة الضلع المقابل للزاوية المحددة إلى الوتر.
- جيب التمام (cos θ) يتم حسابه كنسبة الضلع المجاور للزاوية المحددة إلى الوتر.
- الظل (tan θ) يتم حسابه كنسبة الضلع المقابل للزاوية المحددة إلى الضلع المجاور.
وهذه النسب يمكن استخدامها لحساب المقادير غير المعروفة في المثلثات المختلفة باستخدام الأطوال المعروفة للأضلاع في المثلث.
أما بالنسبة للنسب المثلثية الأخرى (القاطع، وقاطع التمام، وظل التمام)، فهي مقلوبة للنسب الأساسية الثلاثة وتمثل العكس المتبادل لها.
اقرأ أيضًا: برامج تعلم اللغة الانجليزية من الصفر مجانا
أمثلة على المتطابقات المثلثية
هذه بعض المتطابقات المثلثية المهمة التي تستخدم بشكل شائع في حل المسائل الهندسية والرياضية التي تتعلق بالمثلثات. إليك شرح لبعضها:
متطابقات فيثاغورس المثلثية:
- \( \sin^2(\theta) + \cos^2(\theta) = 1 \) هذه المتطابقة تعبر عن العلاقة بين جيب وجيب التمام في المثلث القائم الزاوية.
- \( 1 + \tan^2(\theta) = \sec^2(\theta) \) هذه المتطابقة تربط بين الظل والقاطع في المثلث القائم الزاوية.
- \( 1 + \cot^2(\theta) = \csc^2(\theta) \) هذه المتطابقة تربط بين ظل التمام وقاطع التمام في المثلث القائم الزاوية.
المتطابقات المثلثية للزوايا المضاعفة:
- \( \sin(2\theta) = 2 \sin(\theta) \cos(\theta) \) تُستخدم هذه المتطابقة لحساب الجيب لزاوية مضاعفة.
- \( \cos(2\theta) = \cos^2(\theta) – \sin^2(\theta) \) تُستخدم هذه المتطابقة لحساب جيب التمام لزاوية مضاعفة.
- \( \tan(2\theta) = \frac{2 \tan(\theta)}{1 – \tan^2(\theta)} \) تُستخدم هذه المتطابقة لحساب الظل لزاوية مضاعفة.
هذه المتطابقات تسهل عملية حساب القيم المثلثية للزوايا والأطوال في المثلثات وتساعد في حل مجموعة واسعة من المسائل الهندسية.
اقرأ أيضًا: بحث عن العمل الحر ومجالاته وسلبياته
ما هو حساب المثلثات؟
علم حساب المثلثات هو فرع من الرياضيات يركز على دراسة العلاقات والخصائص المتعلقة بالمثلثات، بما في ذلك الأطوال الجانبية والزوايا، يعتبر حساب المثلثات أحد الأسس الأساسية في العديد من التطبيقات العملية والفروع الأخرى للرياضيات والعلوم.
يشمل علم حساب المثلثات مجموعة متنوعة من المفاهيم، بما في ذلك:
- حساب الأطوال الجانبية للمثلثات باستخدام مفاهيم الجيومتريا والجبر.
- قياس وتحديد الزوايا في المثلثات باستخدام الدوال المثلثية مثل الجيب وجيب التمام وظل الزاوية.
- استخدام المثلثات في حساب المسافات والأرتفاعات في الهندسة المدنية والعلوم الطبيعية.
- تطبيقات في المجالات التقنية مثل الإلكترونيات والرادار والبصريات.
باختصار، علم حساب المثلثات له تطبيقات عملية متعددة في الحياة اليومية والعديد من المجالات الفنية والعلمية، كما يمثل أساساً مهماً في الرياضيات ويُستخدم بشكل واسع في العديد من المجالات العملية والتطبيقية المختلفة والضرورية في الحياه.





