بحث عن المثلث يعتبر كتابة بحث عن المثلث امر هام حيث أن المثلث هو أحد الأشكال الهندسية الأساسية، يتكون من ثلاثة رؤوس وثلاثة أضلاع تصل بينها، تتكون الأضلاع في المثلث من قطع مستقيمة، يشترط في المثلث أن يكون مجموع طولي أي ضلعين أكبر من طول الضلع الثالث لكي يكون مثلثًا صالحا.
بحث عن المثلث
إليك بعض المصطلحات المهمة المتعلقة بالمثلث:
- الرأس (Vertex): هو الزاوية في المثلث، وكل مثلث يحتوي على ثلاثة أرؤس.
- القاعدة (Base): يمكن لأي ضلع في المثلث أن يكون قاعدة، وعادة ما يكون الضلع الموجود في الجزء السفلي من المثلث هو القاعدة، في المثلث المتساوي الأضلاع، القاعدة هي الضلع الذي ليس متساوي الطول مع الضلعين الآخرين.
- المتوسط (Median): هو الخط الذي يمتد من رأس المثلث إلى منتصف الضلع المقابل له ويحتوي كل مثلث على ثلاثة متوسطات، وتتقاطع في نقطة واحدة تسمى مركز المثلث.
- الارتفاع (Altitude): هو الخط العمودي الممتد من أحد رؤوس المثلث إلى الضلع المقابل له. يمكن أن يكون هناك ثلاثة أرتفاعات مختلفة في المثلث، وتتقاطع في نقطة تسمى مركز الارتفاعات أو المركز القائم.
هذه المصطلحات مهمة جداً لفهم خصائص المثلثات وتطبيقاتها في الرياضيات والهندسة.
خصائص المثلث
إليكم بعض الخصائص الهامة الإضافية للمثلث:
- تقسيم المثلث: عند رسم مستقيم يمر بواحد من أضلاع المثلث ويقطع الضلعين الآخرين، يتم تقسيم المثلث إلى مثلثات متشابهة ومتناسبة في الطول، هذا يعني أن نسب الأضلاع في هذه المثلثات الصغيرة متساوية.
- قوانين الضلوع: مجموع أطوال أي ضلعين من المثلث دائماً أكبر من طول الضلع الثالث. بالمثل، فإن الفرق بين أطوال أي ضلعين أقل من طول الضلع الثالث.
- الزوايا الخارجية: زاوية خارجية للمثلث تساوي مجموع الزوايا الداخلية المقابلة لها أو البعيدة عنها، مجموع الزوايا الخارجية للمثلث هو دائماً 360 درجة.
- الارتفاعات والمتوسطات: الارتفاع المثلثي يقسم المثلث متساوي الساقين والمثلث متساوي الأضلاع القاعدة إلى نصفين متساويين، بالإضافة إلى ذلك، المثلث يمكن أن يقسم إلى مثلثين متساويين عند تمرير متوسط من أحد رؤوس المثلث إلى منتصف الضلع المقابل له.
هذه الخصائص تعتبر أساسية في فهم المثلثات والتعامل معها في الرياضيات والهندسة.
اقرأ أيضًا: بحث كامل عن حقوق الإنسان مع المراجع
أنواع المثلثات
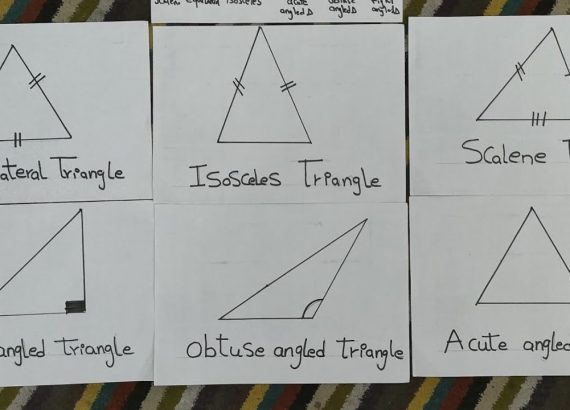
تم توضيح أنواع المثلثات حسب طول الأضلاع على النحو التالي:
- المثلث متساوي الأضلاع: يتميز بأن جميع أضلاعه ذات طول متساوٍ، كل زاوية داخلية في هذا المثلث تقيس 60 درجة، وهو يمثل في الغالب بواسطة رمز الخطوط المائلة على الأضلاع.
- المثلث متساوي الساقين: يتميز بأن لديه زوجان من الأضلاع ذات الطول المتساوي، وزاويتان متساويتان، الضلعان ذات الطول المتساوي عادةً ما يكونان الضلعين غير القاعدة.
- المثلث مختلف الأضلاع: لا يتمتع بأي أضلاع متساوية في الطول، ولا بأي زوايا متساوية في القياس.
تم تقسيم المثلثات حسب الزوايا كما يلي:
- المثلث حاد الزوايا: يكون جميع زواياه أقل من 90 درجة، أي أن جميع زواياه حادة.
- المثلث قائم الزوايا: يحتوي على زاوية قائمة قياسها 90 درجة ومن أنواع المثلثات القائمة الخاصة:
- مثلث 90-45-45: يحتوي على زاوية قائمة وزاويتان متساويتان قياسهما 45 درجة، ويكون ذو ضلعين متساويين، يمكن استخدام نظرية فيثاغورس لحساب أطوال الأضلاع.
- مثلث 90-60-30: يحتوي على زاوية قائمة وزاويتان أخريان بقياس 60 درجة و 30 درجة على التوالي، يكون ذو ضلعين متناسبين بنسبة 1: 3√: 2.
- المثلث منفرج الزاوية: يحتوي على زاوية واحدة أكبر من 90 درجة، وتسمى هذه الزاوية المنفرجة.
هذه هي الأنواع الثلاثة الرئيسية للمثلثات حسب الزوايا، ويمكن استخدام خصائص كل نوع لحساب مختلف الأبعاد والزوايا للمثلث.
اقرأ أيضًا: بحث عن العمل التطوعي وفوائده ومميزاته
أمثلة متنوعة حول أنواع المثلثات
سنتحدث عن الأمثلة كما يلي:
- المثال الأول: المثلث الذي يحتوي على زاوية بقياس 115 درجة هو مثلث منفرج الزاوية.
- المثال الثاني: المثلث الذي يحتوي على زاوية بقياس 112 درجة هو أيضًا مثلث منفرج الزاوية.
- المثال الثالث: بما أن أطوال الأضلاع مختلفة (5، 12، 13) فإن هذا المثلث هو مثلث مختلف الأضلاع.
- المثال الرابع: المثلث الذي يحتوي على زوايا بقياسات 46، 63، و 71 درجة هو مثلث حاد الزوايا، لأن قياس كل زاوية من زواياه أقل من 90 درجة.
يتم تمييز المثلث برموز تعبر عن رؤوسه، على سبيل المثال، إذا كانت رؤوس المثلث هي A و B و C، فيمكن تمثيله بالرمز \( \triangle ABC \).





