بحث عن المثلثات المتطابقة سنقدم الآن بحث عن المثلثات المتطابقة حيث أن المثلث هو شكل ثنائي الأبعاد يتألف من ثلاثة أضلاع وثلاث زوايا وثلاثة رؤوس، يعتبر المثلثان متطابقان عندما يتشابها في الشكل والحجم، بحيث تكون الأضلاع المتقابلة متساوية الطول، أو الزوايا المتقابلة متساوية.
جدول المحتويات
بحث عن المثلثات المتطابقة
يمكن حساب مساحة ومحيط المثلث بنفس الطريقة المستخدمة في حساب أي شكل هندسي آخر، ويُستخدم ذلك في التطبيقات الهندسية المختلفة في بعض الحالات، قد تتطابق أو تتشابه مجموعات من المثلثات إذا تحققت لها مجموعة من الشروط المتعلقة بأطوال الأضلاع وقياسات الزوايا.
التطابق بشكل عام يشير إلى وجود كائنين وصورتهما المعكوسة، حيث يمكن وضعهما فوق بعضهما بدون تغيير في الشكل.
تطابق المثلثات يحدث عندما يتشابها مثلثان في الشكل والحجم، ويتضمن ذلك:
- تساوي أطوال الأضلاع الثلاثة المتناظرة.
- تساوي قياسات الزوايا الثلاث المتناظرة.
بالتالي، يمكن نقل هذه المثلثات، وتدويرها، وعكسها، وتحويلها لتتماشى مع بعضها البعض دون تغيير في التطابق، علامة التطابق بين المثلثات هي (≅).
عندما تكون المثلثات متطابقة، يكون لها المواصفات التالية:
- مساحات متساوية.
- محيطات متساوية.
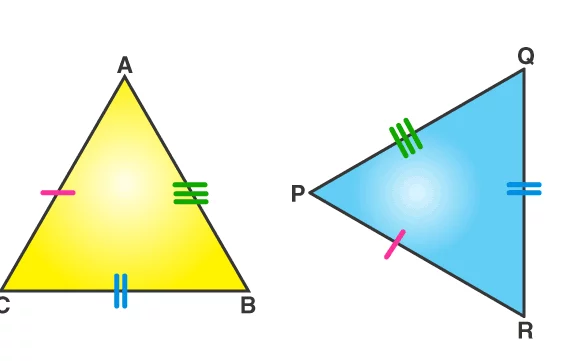
حالات المثلثات المتطابقة
يتم تحديد تطابق المثلثان عندما تتحقق إحدى الحالات التالية:
- SSS (Side-Side-Side): يتطابق المثلثان عندما تكون أطوال الأضلاع في المثلث الأول متساوية لأطوال الأضلاع المتناظرة لها في المثلث الثاني في هذه الحالة، يجب أن تتساوى الزوايا المتقابلة أيضًا.
- ASA (Angle-Side-Angle): يتطابق المثلثان عندما يكون طول ضلعين وقياس الزاوية بينهما في المثلث الأول متساويًا مع طول الضلعين المقابلين وقياس الزاوية بينهما في المثلث الثاني وفي هذه الحالة، يجب أن يتساوى الضلع الثالث وقياس الزاويتين الأخريين.
- AAS (Angle-Angle-Side): يتطابق المثلثان عندما يكون قياس زاويتين مع طول الضلع المشترك بينهما في المثلث الأول مساويًا لقياس نفس الزاويتين المتقابلتين في المثلث الثاني مع طول الضلع بينهما وفي هذه الحالة، يجب أن تتساوى قياس الزاوية الثالثة وطول الضلعين الآخرين.
اقرأ أيضًا: بحث عن العمل الجماعي وعناصره وقوانينه
خصائص المثلثات المتطابقة
عندما تكون المثلثات متطابقة، فإنها تمتلك عدة خصائص، وهي كما يلي:
- تساوي جميع أطوال الأضلاع وقياسات الزوايا في المثلث الأول المثلث الثاني وبالتالي، يمكن حساب طول أي ضلع مجهول أو قياس زاوية مجهولة في أحد المثلثين استنادًا إلى المثلث الآخر.
- تماثل جميع خصائص المثلث الأول خصائص المثلث الثاني، بما في ذلك مساحتهما، ومحيطهما، ومركز المثلث، والدوائر المرتبطة بهما، وغيرها من الخصائص.
إثبات تطابق المثلثين
عند إثبات تطابق المثلثات، ليس من الضرورة إثبات جميع الحقائق الستة لإظهار التطابق يكفي إثبات حالة واحدة من الحالات المذكورة سابقًا لإظهار أن المثلثين متطابقان، ومن ثم يمكن استنتاج الحقائق الأخرى. يمكن أن تكون هذه الحالات كما يلي:
- إثبات تطابق الأضلاع: عندما تتطابق أطوال الأضلاع الثلاثة لأحد المثلثين مع الأضلاع المتناظرة في المثلث الآخر، يتبين تطابق المثلثين، مما يدل على مساواة قياسات الزوايا.
- إثبات تطابق الضلعين والزاوية: عندما تتساوى أطوال ضلعين في أحد المثلثين مع الضلعين المتناظرين في المثلث الآخر، وتتساوى قياسات الزوايا المحصورة بينهما، يتبين تطابق المثلثين ومساواة الضلع الثالث والزوايتين الأخريتين.
- إثبات تطابق الزوايتين والضلع المتضمن: عندما تتطابق قياسات زاويتين في أحد المثلثين مع الزوايا المتناظرة في المثلث الآخر، ويتطابق الضلع المتضمن بينهما، يتبين تطابق المثلثين ومساواة الزاوية الثالثة والضلعين الآخرين.
- إثبات تطابق الزاويتين والضلع المشترك: عندما تتطابق قياسات زاويتين في أحد المثلثين مع الزوايا المتناظرة في المثلث الآخر، ويتطابق الضلع المشترك بينهما، يتبين تطابق المثلثين.
- إثبات تطابق المثلثات القائمة: عندما يتطابق مثلث قائم الزاوية مع مثلث قائم آخر، ويتساوى طول الوتر والضلع في كل منهما، يتبين تطابق المثلثين ومساواة الضلع الثالث وقياسات الزاويتين الأخريتين.
باختصار، يمكن إثبات أي من هذه الحالات لتوضيح تطابق المثلثين دون الحاجة إلى إثبات كل الحقائق الستة.
اقرأ أيضًا: بحث عن العمل الحر ومجالاته وسلبياته
المثلث في علم الهندسة هو شكل ثنائي الأبعاد يتألف من ثلاثة أضلاع وثلاثة زوايا، حيث يتوجب أن يكون مجموع قياس زواياه ١٨٠ درجة، يوجد أنواع مختلفة من المثلثات في علم الهندسة، تختلف وفقًا لقياسات الزوايا وأطوال الأضلاع، يعتبر المثلث من الأشكال الهندسية الأساسية والمهمة في علم الرياضيات، حيث يستخدم في تشكيل الأشكال الهرمية ويُدمج في تصميم العديد من المشاريع الهندسية.





