بحث عن ميل المستقيم،يعرف الميل الزاوية التي يصنعها الخط المستقيم مع الأفقي أو الرأسي، ويتم قياسه بوحدة الزاوية مثل الدرجة أو الراديان تعتبر مفاهيم الميل أساسية في العديد من المجالات مثل الهندسة المدنية والهندسة الميكانيكية وعلوم الجغرافيا، حيث يستخدم لتحديد اتجاهات الخطوط والأسطح والمنحنيات،على سبيل المثال، في الهندسة المدنية، يستخدم الميل لتحديد اتجاهات الطرق والجسور والأنفاق، بينما في الهندسة الميكانيكية يستخدم لتحديد اتجاهات الأجزاء الميكانيكية والآلات.
تاريخ ميل المستقيم
- تاريخ مفهوم ميل المستقيم يعود إلى العصور القديمة حيث كان يستخدم في الهندسة والعمارة، يمكن رؤية استخداماته في العمارة القديمة مثل المعابد والهرمات حيث كان يستخدم لتحديد اتجاه الهياكل وتصميم الأسطح بشكل مائل لتوفير تصريف المياه ولأسباب جمالية.
- في العصور القديمة، كانت المفاهيم الهندسية بسيطة نسبيا وكانت تستند إلى الملاحظات والتجارب العملية على سبيل المثال، في مصر القديمة، كان الهندسيون يستخدمون النجوم وظاهرة الظل لتحديد الاتجاهات وتصميم الهياكل المعمارية.
- مع تطور الرياضيات والهندسة في العصور الوسطى والعصور الحديثة، تطور فهمنا لمفهوم الميل المستقيم وتوسعت استخداماته،وفي القرن العشرين، مع تقدم التكنولوجيا والهندسة، أصبحت مفاهيم الميل والزوايا تدرس بشكل أكثر تطوراً ودقة، وأصبح لها تطبيقات متنوعة في مجالات مثل الهندسة المدنية والهندسة الميكانيكية والجغرافيا.
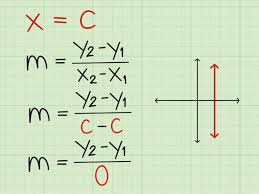
اقرأ أيضًا: رابط تسجيل الدخول بلاك بورد جامعة الطائف
طرق حساب ميل المستقيم
هناك عدة طرق لحساب ميل المستقيم، وتتضمن هذه الطرق الحسابية المباشرة والرياضية إليك بعض الطرق الشائعة لحساب ميل المستقيم:
- استخدام نقطتين على المستقيم: يمكن حساب ميل المستقيم باستخدام إحداثيات نقطتين على المستقيم، يتم ذلك عن طريق حساب الفرق في الإحداثيات العمودية والأفقية بين النقطتين، ثم استخدام العلاقة التالية:
ميل المستقيم = (الارتفاع العمودي) ÷ (الانفراج الأفقي)
- استخدام الميل والزاوية: في بعض الحالات، يمكن حساب ميل المستقيم باستخدام الميل والزاوية الأفقية أو الرأسية. في هذه الحالة، يكون ميل المستقيم هو المثلثية للزاوية.
- استخدام المعادلة الرياضية: يمكن استخدام المعادلات الرياضية لحساب ميل المستقيم إذا كانت معادلة المستقيم معروفة، يتم ذلك عن طريق حساب المشتقة الأولى للمعادلة واستخراج الميل منها.
الخصائص الهامة لميل المستقيم
إليك بعض الخصائص الهامة لميل المستقيم:
- الميل والزوايا: ميل المستقيم يُعرف عادةً كنسبة الارتفاع العمودي إلى الانفراج الأفقي، وهو أيضًا يمثل المثلثية للزاوية التي يجعلها المستقيم مع الأفق.
- الاتجاه: الميل يحدد الاتجاه الذي يأخذه المستقيم عندما ينحرف عن الأفقي أو الرأسي، إذا كان الميل إيجابيا، فإن المستقيم يميل باتجاه معين بعيدا عن الأفق، أما إذا كان سالبًا، فإنه يميل في الاتجاه المعاكس.
- التوازي والعمودية: المستقيمان الذين لهما نفس الميل يعتبران متوازيين، في حين يكونان عموديين على بعضهما البعض إذا كانا متقاطعين ويُشكل كل واحد منهما زاوية قائمة مع الآخر.
- الميل المتغير: يمكن للمستقيم أن يتغير ميله على طول طوله، ويكون ذلك في حالات مثل المنحنيات والانحناءات.
- الميل والمسافة: يمكن استخدام ميل المستقيم مع المسافة بين نقطتين لحساب الارتفاع العمودي أو الانفراج الأفقي بينهما.
- العلاقة بالمعادلات الرياضية: يمكن تحديد ميل المستقيم باستخدام المعادلات الرياضية للمستقيم، وعادة ما يتم استخدام المشتقة الأولى للمعادلة لحساب الميل.
اقرأ أيضًا: شروط وطريقة التسجيل في الضمان الاجتماعي المطور للمعاقين
في الختام، يظهر ميل المستقيم أهمية كبيرة في الرياضيات والهندسة والعديد من المجالات الأخرى،يستخدم هذا المفهوم لتحديد اتجاهات الخطوط والأسطح والمنحنيات، وهو يعتبر أساسيا في تحليل وتصميم الهياكل والأنظمة في الهندسة المدنية والهندسة الميكانيكية والجغرافيا،بفضل خصائصه وتطبيقاته المتعددة، يساهم ميل المستقيم في فهمنا للعالم المحيط وتطوير التقنيات والتطبيقات العملية.





